العدد العقدي أو العدد المركب هو أي عدد على الصورة: حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.
و عندما يكون b (أي الجزء التخيلي) = 0، فإن قيمة العدد العقدي تساوي قيمة الجزء الحقيقي a فقط و سمي العدد عددًا حقيقيـًا صرفًا Purely real. و عندما يكون a (أي الجزء الحقيقي) = 0، كان العدد تخيليـًا صرفـًا Purely imaginary.
من الممكن إجراء العمليات الحسابية العادية على الأعداد العقدية، كالجمع و الطرح و القسمة و الضرب، تمامًا كالأعداد الحقيقية، و لكنها أيضـًا تتمتع بخصائص أخرى تمكنها من حل كافة المعادلات الجبرية العادية التي يصعب حلها باستخدام الأعداد الحقيقية فقط.
و أحيانـًا قد يكتب العدد العقدي z على الصورة z = a + bj (خصوصـًا في مجال الهندسة الكهربية، لأن i هو رمز التيار الكهربي)

التعريف
إذا فرضنا أن z هو عدد مركب، و a و b هما عددان حقيقيان، و i هو عدد تخيلي، فمن الممكن تمثيل العدد المركب z كما يلي:

تمثيل الأعداد المركبة
يكتب العدد المركب z جبريًا بالشكل:

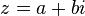
التمثيل الجبري
يكتب العدد على شكل

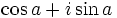
التمثيل الهندسي
يكتب العدد على شكل

التمثيل الأسي

الحساب في مجموعة الأعداد العقدية
تتم عملية الجمع كما يلي:


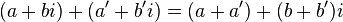
الجمع
تتم عملية الضرب كما يلي


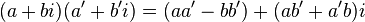
الضرب
تتم عملية القسمة كما يلي:


مرافق عدد عقدي
مرافق العدد العقدي هو العدد العقدي .
مرافق العدد العقدي z نرمز له ب:

تعريف

مرافق مجموع عددين عقديين هو مجموع مرافق كل من حدي المجموع
مرافق جداء عددين عقديين هو جداء مرافق كل من حدي الجداء الأعداد المترافقة و العمليات
جدر مربع جداء عدد عقدي في مرافقه يسمى معيار العدد العقدي

التمثيل الهندسي للأعداد العقدية
المستوى 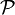منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من 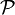التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي يسمى 'لحق' النقطة M.